Linear Adversarial Concept Erasure

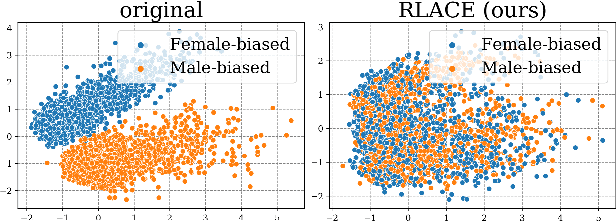
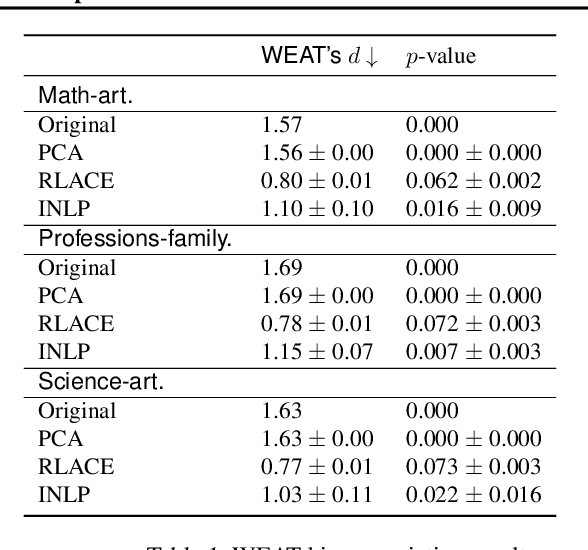
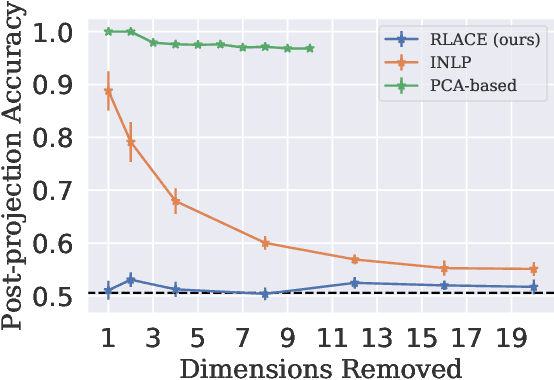
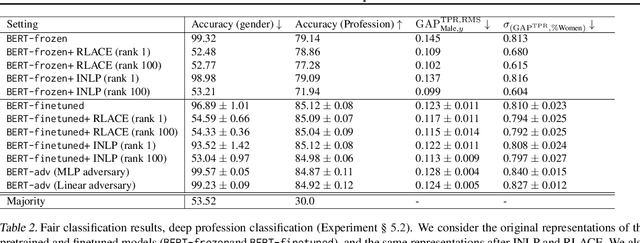
Modern neural models trained on textual data rely on pre-trained representations that emerge without direct supervision. As these representations are increasingly being used in real-world applications, the inability to \emph{control} their content becomes an increasingly important problem. We formulate the problem of identifying and erasing a linear subspace that corresponds to a given concept, in order to prevent linear predictors from recovering the concept. We model this problem as a constrained, linear minimax game, and show that existing solutions are generally not optimal for this task. We derive a closed-form solution for certain objectives, and propose a convex relaxation, R-LACE, that works well for others. When evaluated in the context of binary gender removal, the method recovers a low-dimensional subspace whose removal mitigates bias by intrinsic and extrinsic evaluation. We show that the method -- despite being linear -- is highly expressive, effectively mitigating bias in deep nonlinear classifiers while maintaining tractability and interpretability.

Null It Out: Guarding Protected Attributes by Iterative Nullspace Projection

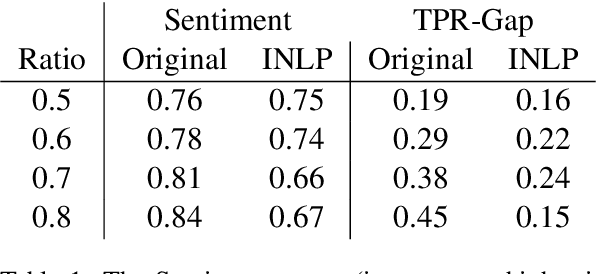
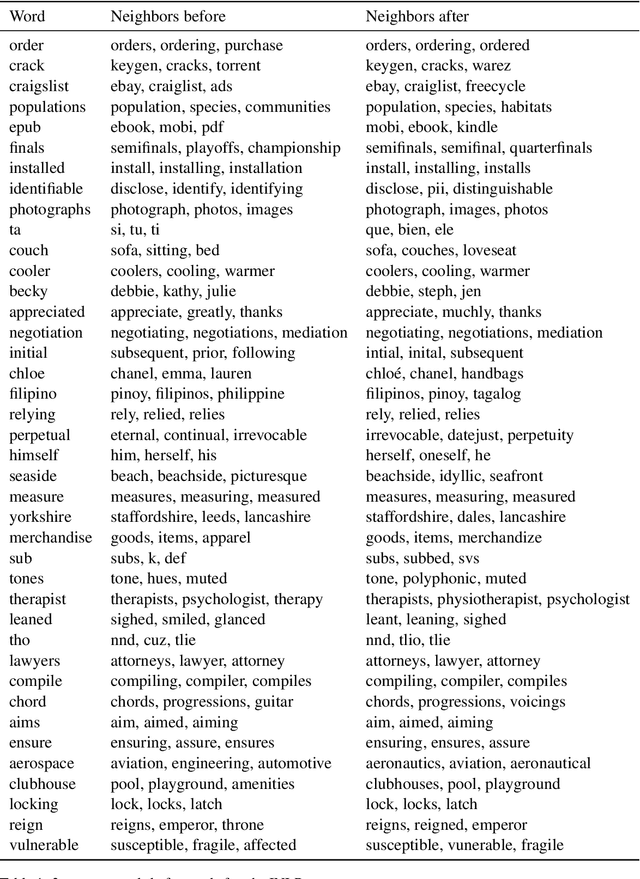
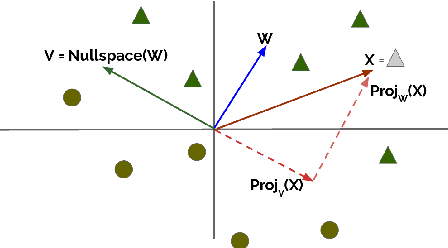
The ability to control for the kinds of information encoded in neural representation has a variety of use cases, especially in light of the challenge of interpreting these models. We present Iterative Null-space Projection (INLP), a novel method for removing information from neural representations. Our method is based on repeated training of linear classifiers that predict a certain property we aim to remove, followed by projection of the representations on their null-space. By doing so, the classifiers become oblivious to that target property, making it hard to linearly separate the data according to it. While applicable for multiple uses, we evaluate our method on bias and fairness use-cases, and show that our method is able to mitigate bias in word embeddings, as well as to increase fairness in a setting of multi-class classification.